Snell's Law
The refraction is described by Snell’s law:
\[ \eta \cdot \sin \theta = \eta' \cdot \sin \theta' \]
Where \( \theta \) and \( \theta' \) are the angles from the normal, and \( \eta \) and \( \eta' \) (pronounced “eta” and “eta prime”) are the refractive indices. The geometry is:
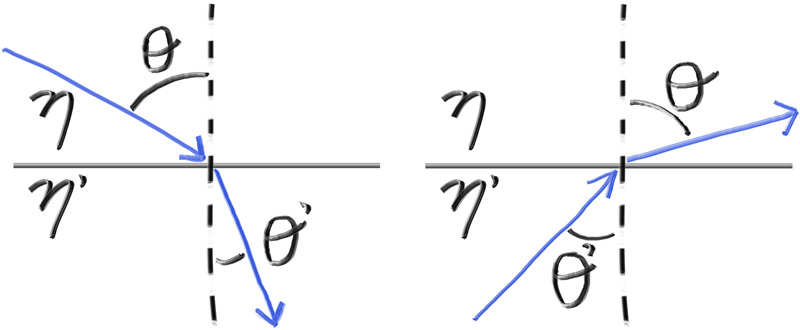
Figure 17: Ray refraction
In order to determine the direction of the refracted ray, we have to solve for \( \sin \theta' \):
\[ \sin \theta' = \frac{\eta}{\eta'} \cdot \sin \theta \]
On the refracted side of the surface there is a refracted ray \( \mathbf{R}' \) and a normal \( \mathbf{n}' \), and there exists an angle, \( \theta' \), between them. We can split \( \mathbf{R}' \) into the parts of the ray that are perpendicular to \( \mathbf{n}' \) and parallel to \( \mathbf{n}' \):
\[ \mathbf{R}' = \mathbf{R}' _ {\bot} + \mathbf{R}'_{\|} \]
If we solve for \( \mathbf{R}' _ {\bot} \) and \( \mathbf{R}'_{\|} \) we get:
\[ \mathbf{R}' _ {\bot} = \frac{\eta}{\eta'} (\mathbf{R} + |\mathbf{R}| \cos( \theta ) \mathbf{n} ) \]
\[ \mathbf{R}'_{\|} = - \sqrt{1 - |\mathbf{R}' _ {\bot}|^2 } \mathbf{n} \]
You can go ahead and prove this for yourself if you want, but we will treat it as fact and move on. The rest of the book will not require you to understand the proof.
We know the value of every term on the right-hand side except for \( \cos \theta \). It is well known that the dot product of two vectors can be explained in terms of the cosine of the angle between them:
\[ \mathbf{𝐚} \cdot \mathbf{b} = |\mathbf{a}| |\mathbf{b}| \cos \theta \]
If we restrict \( \mathbf{a} \) and \( \mathbf{b} \) to be unit vectors:
\[ \mathbf{𝐚} \cdot \mathbf{b} = \cos \theta \]
We can now rewrite \( \mathbf{R}' _ {\bot} \) in terms of known quantities:
\[ \mathbf{R}' _ {\bot} = \frac{\eta}{\eta'} (\mathbf{R} + (- \mathbf{R} \cdot \mathbf{n} ) \mathbf{n} ) \]
When we combine them back together, we can write a function to calculate \( \mathbf{R}' \):
diff --git a/src/vec3.rs b/src/vec3.rs
index 4cb0b6f..62afd80 100644
--- a/src/vec3.rs
+++ b/src/vec3.rs
@@ -1,234 +1,243 @@
use std::{
fmt::Display,
ops::{Add, AddAssign, Div, DivAssign, Index, IndexMut, Mul, MulAssign, Neg, Sub},
};
#[derive(Debug, Default, Clone, Copy)]
pub struct Vec3 {
pub e: [f64; 3],
}
pub type Point3 = Vec3;
impl Vec3 {
pub fn new(e0: f64, e1: f64, e2: f64) -> Self {
Self { e: [e0, e1, e2] }
}
pub fn x(&self) -> f64 {
self.e[0]
}
pub fn y(&self) -> f64 {
self.e[1]
}
pub fn z(&self) -> f64 {
self.e[2]
}
pub fn length(&self) -> f64 {
f64::sqrt(self.length_squared())
}
pub fn length_squared(&self) -> f64 {
self.e[0] * self.e[0] + self.e[1] * self.e[1] + self.e[2] * self.e[2]
}
pub fn near_zero(&self) -> bool {
// Return true if the vector is close to zero in all dimensions.
const S: f64 = 1e-8;
self.e[0].abs() < S && self.e[1].abs() < S && self.e[2].abs() < S
}
pub fn random() -> Self {
Vec3 { e: rand::random() }
}
pub fn random_range(min: f64, max: f64) -> Self {
Vec3::new(
rand::random_range(min..max),
rand::random_range(min..max),
rand::random_range(min..max),
)
}
}
impl Neg for Vec3 {
type Output = Self;
fn neg(self) -> Self::Output {
Self::Output {
e: self.e.map(|e| -e),
}
}
}
impl Index<usize> for Vec3 {
type Output = f64;
fn index(&self, index: usize) -> &Self::Output {
&self.e[index]
}
}
impl IndexMut<usize> for Vec3 {
fn index_mut(&mut self, index: usize) -> &mut Self::Output {
&mut self.e[index]
}
}
impl AddAssign for Vec3 {
fn add_assign(&mut self, rhs: Self) {
self.e[0] += rhs.e[0];
self.e[1] += rhs.e[1];
self.e[2] += rhs.e[2];
}
}
impl MulAssign<f64> for Vec3 {
fn mul_assign(&mut self, rhs: f64) {
self.e[0] *= rhs;
self.e[1] *= rhs;
self.e[2] *= rhs;
}
}
impl DivAssign<f64> for Vec3 {
fn div_assign(&mut self, rhs: f64) {
self.mul_assign(1.0 / rhs);
}
}
impl Display for Vec3 {
fn fmt(&self, f: &mut std::fmt::Formatter<'_>) -> std::fmt::Result {
write!(f, "{} {} {}", self.e[0], self.e[1], self.e[2])
}
}
impl Add for Vec3 {
type Output = Self;
fn add(self, rhs: Self) -> Self::Output {
Self::Output {
e: [
self.e[0] + rhs.e[0],
self.e[1] + rhs.e[1],
self.e[2] + rhs.e[2],
],
}
}
}
impl Sub for Vec3 {
type Output = Self;
fn sub(self, rhs: Self) -> Self::Output {
Self::Output {
e: [
self.e[0] - rhs.e[0],
self.e[1] - rhs.e[1],
self.e[2] - rhs.e[2],
],
}
}
}
impl Mul for Vec3 {
type Output = Self;
fn mul(self, rhs: Self) -> Self::Output {
Self::Output {
e: [
self.e[0] * rhs.e[0],
self.e[1] * rhs.e[1],
self.e[2] * rhs.e[2],
],
}
}
}
impl Mul<f64> for Vec3 {
type Output = Self;
fn mul(self, rhs: f64) -> Self::Output {
Self::Output {
e: [self.e[0] * rhs, self.e[1] * rhs, self.e[2] * rhs],
}
}
}
impl Mul<Vec3> for f64 {
type Output = Vec3;
fn mul(self, rhs: Vec3) -> Self::Output {
rhs.mul(self)
}
}
impl Div<f64> for Vec3 {
type Output = Self;
fn div(self, rhs: f64) -> Self::Output {
self * (1.0 / rhs)
}
}
#[inline]
pub fn dot(u: Vec3, v: Vec3) -> f64 {
u.e[0] * v.e[0] + u.e[1] * v.e[1] + u.e[2] * v.e[2]
}
#[inline]
pub fn cross(u: Vec3, v: Vec3) -> Vec3 {
Vec3::new(
u.e[1] * v.e[2] - u.e[2] * v.e[1],
u.e[2] * v.e[0] - u.e[0] * v.e[2],
u.e[0] * v.e[1] - u.e[1] * v.e[0],
)
}
#[inline]
pub fn unit_vector(v: Vec3) -> Vec3 {
v / v.length()
}
#[inline]
pub fn random_unit_vector() -> Vec3 {
loop {
let p = Vec3::random_range(-1.0, 1.0);
let lensq = p.length_squared();
if 1e-160 < lensq && lensq <= 1.0 {
return p / f64::sqrt(lensq);
}
}
}
#[inline]
pub fn random_on_hemisphere(normal: Vec3) -> Vec3 {
let on_unit_sphere = random_unit_vector();
if dot(on_unit_sphere, normal) > 0.0 {
on_unit_sphere
} else {
-on_unit_sphere
}
}
#[inline]
pub fn reflect(v: Vec3, n: Vec3) -> Vec3 {
v - 2.0 * dot(v, n) * n
}
#[inline]
+pub fn refract(uv: Vec3, n: Vec3, etai_over_etat: f64) -> Vec3 {
+ let cos_theta = f64::min(dot(-uv, n), 1.0);
+ let r_out_perp = etai_over_etat * (uv + cos_theta * n);
+ let r_out_parallel = -f64::sqrt(f64::abs(1.0 - r_out_perp.length_squared())) * n;
+
+ r_out_perp + r_out_parallel
+}
+
+#[inline]
pub fn random_in_unit_disk() -> Vec3 {
loop {
let p = Vec3::new(
rand::random_range(-1.0..1.0),
rand::random_range(-1.0..1.0),
0.0,
);
if p.length_squared() < 1.0 {
return p;
}
}
}Listing 71: [vec3.rs] Refraction function
And the dielectric material that always refracts is:
diff --git a/src/material.rs b/src/material.rs
index e52f6f3..090a4f6 100644
--- a/src/material.rs
+++ b/src/material.rs
@@ -1,58 +1,89 @@
use crate::{hittable::HitRecord, prelude::*};
pub trait Material {
fn scatter(&self, _r_in: Ray, _rec: HitRecord) -> Option<(Ray, Color)> {
None
}
}
#[derive(Debug, Default, Clone, Copy)]
pub struct Lambertian {
albedo: Color,
}
impl Lambertian {
pub fn new(albedo: Color) -> Self {
Self { albedo }
}
}
impl Material for Lambertian {
fn scatter(&self, _r_in: Ray, rec: HitRecord) -> Option<(Ray, Color)> {
let mut scatter_direction = rec.normal + random_unit_vector();
// Catch degenerate scatter direction
if scatter_direction.near_zero() {
scatter_direction = rec.normal;
}
let scattered = Ray::new(rec.p, scatter_direction);
let attenuation = self.albedo;
Some((scattered, attenuation))
}
}
#[derive(Debug, Default, Clone, Copy)]
pub struct Metal {
albedo: Color,
fuzz: f64,
}
impl Metal {
pub fn new(albedo: Color, fuzz: f64) -> Self {
let fuzz = if fuzz < 1.0 { fuzz } else { 1.0 };
Self { albedo, fuzz }
}
}
impl Material for Metal {
fn scatter(&self, r_in: Ray, rec: HitRecord) -> Option<(Ray, Color)> {
let mut reflected = reflect(r_in.direction(), rec.normal);
reflected = unit_vector(reflected) + (self.fuzz * random_unit_vector());
let scattered = Ray::new(rec.p, reflected);
let attenuation = self.albedo;
(dot(scattered.direction(), rec.normal) > 0.0).then(|| (scattered, attenuation))
}
}
+
+#[derive(Debug, Default, Clone, Copy)]
+pub struct Dielectric {
+ /// Refractive index in vacuum or air, or the ratio of the material's refractive index over
+ /// the refractive index of the enclosing media
+ refraction_index: f64,
+}
+
+impl Dielectric {
+ pub fn new(refraction_index: f64) -> Self {
+ Self { refraction_index }
+ }
+}
+
+impl Material for Dielectric {
+ fn scatter(&self, r_in: Ray, rec: HitRecord) -> Option<(Ray, Color)> {
+ let attenuation = Color::new(1.0, 1.0, 1.0);
+ let ri = if rec.front_face {
+ 1.0 / self.refraction_index
+ } else {
+ self.refraction_index
+ };
+
+ let unit_direction = unit_vector(r_in.direction());
+ let refracted = refract(unit_direction, rec.normal, ri);
+
+ let scattered = Ray::new(rec.p, refracted);
+
+ Some((scattered, attenuation))
+ }
+}Listing 72: [material.rs] Dielectric material class that always refracts
Now we'll update the scene to illustrate refraction by changing the left sphere to glass, which has an index of refraction of approximately 1.5.
diff --git a/src/main.rs b/src/main.rs
index a705a06..3894014 100644
--- a/src/main.rs
+++ b/src/main.rs
@@ -1,46 +1,46 @@
use code::{
camera::Camera,
hittable_list::HittableList,
- material::{Lambertian, Metal},
+ material::{Dielectric, Lambertian, Metal},
prelude::*,
sphere::Sphere,
};
fn main() -> std::io::Result<()> {
let mut world = HittableList::new();
let material_ground = Rc::new(Lambertian::new(Color::new(0.8, 0.8, 0.0)));
let material_center = Rc::new(Lambertian::new(Color::new(0.1, 0.2, 0.5)));
- let material_left = Rc::new(Metal::new(Color::new(0.8, 0.8, 0.8), 0.3));
+ let material_left = Rc::new(Dielectric::new(1.5));
let material_right = Rc::new(Metal::new(Color::new(0.8, 0.6, 0.2), 1.0));
world.add(Rc::new(Sphere::new(
Point3::new(0.0, -100.5, -1.0),
100.0,
material_ground,
)));
world.add(Rc::new(Sphere::new(
Point3::new(0.0, 0.0, -1.2),
0.5,
material_center,
)));
world.add(Rc::new(Sphere::new(
Point3::new(-1.0, 0.0, -1.0),
0.5,
material_left,
)));
world.add(Rc::new(Sphere::new(
Point3::new(1.0, 0.0, -1.0),
0.5,
material_right,
)));
env_logger::init();
Camera::default()
.with_aspect_ratio(16.0 / 9.0)
.with_image_width(400)
.with_samples_per_pixel(100)
.with_max_depth(50)
.render(&world)
}Listing 73: [main.rs] Changing the left sphere to glass
This gives us the following result:

Image 16: Glass sphere that always refracts