Ray Tracing in One Weekend (Rust)

A Simple Diffuse Material

Diffuse objects that don’t emit their own light merely take on the color of their surroundings, but they do modulate that with their own intrinsic color. Light that reflects off a diffuse surface has its direction randomized, so, if we send three rays into a crack between two diffuse surfaces they will each have different random behavior:

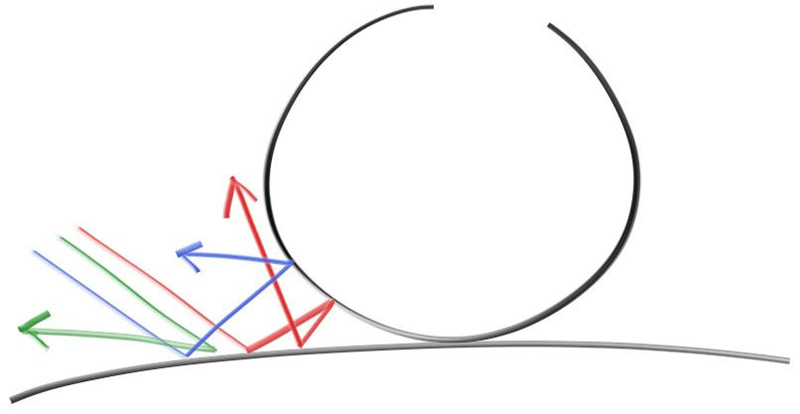
Figure 9: Light ray bounces

They might also be absorbed rather than reflected. The darker the surface, the more likely the ray is absorbed (that’s why it's dark!). Really any algorithm that randomizes direction will produce surfaces that look matte. Let's start with the most intuitive: a surface that randomly bounces a ray equally in all directions. For this material, a ray that hits the surface has an equal probability of bouncing in any direction away from the surface.

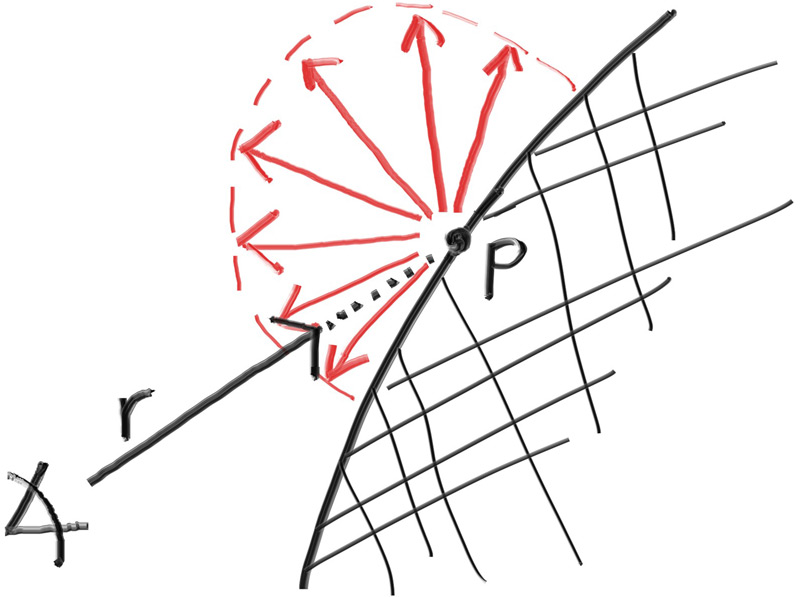
Figure 10: Equal reflection above the horizon

This very intuitive material is the simplest kind of diffuse and — indeed — many of the first raytracing papers used this diffuse method (before adopting a more accurate method that we'll be implementing a little bit later). We don't currently have a way to randomly reflect a ray, so we'll need to add a few functions to our vector utility header. The first thing we need is the ability to generate arbitrary random vectors:

diff --git a/src/vec3.rs b/src/vec3.rs
index d4352e1..f9228ac 100644
--- a/src/vec3.rs
+++ b/src/vec3.rs
@@ -1,190 +1,202 @@
 use std::{
     fmt::Display,
     ops::{Add, AddAssign, Div, DivAssign, Index, IndexMut, Mul, MulAssign, Neg, Sub},
 };
 
 #[derive(Debug, Default, Clone, Copy)]
 pub struct Vec3 {
     pub e: [f64; 3],
 }
 
 pub type Point3 = Vec3;
 
 impl Vec3 {
     pub fn new(e0: f64, e1: f64, e2: f64) -> Self {
         Self { e: [e0, e1, e2] }
     }
 
     pub fn x(&self) -> f64 {
         self.e[0]
     }
 
     pub fn y(&self) -> f64 {
         self.e[1]
     }
 
     pub fn z(&self) -> f64 {
         self.e[2]
     }
 
     pub fn length(&self) -> f64 {
         f64::sqrt(self.length_squared())
     }
 
     pub fn length_squared(&self) -> f64 {
         self.e[0] * self.e[0] + self.e[1] * self.e[1] + self.e[2] * self.e[2]
     }
+
+    pub fn random() -> Self {
+        Vec3 { e: rand::random() }
+    }
+
+    pub fn random_range(min: f64, max: f64) -> Self {
+        Vec3::new(
+            rand::random_range(min..max),
+            rand::random_range(min..max),
+            rand::random_range(min..max),
+        )
+    }
 }
 
 impl Neg for Vec3 {
     type Output = Self;
 
     fn neg(self) -> Self::Output {
         Self::Output {
             e: self.e.map(|e| -e),
         }
     }
 }
 
 impl Index<usize> for Vec3 {
     type Output = f64;
 
     fn index(&self, index: usize) -> &Self::Output {
         &self.e[index]
     }
 }
 
 impl IndexMut<usize> for Vec3 {
     fn index_mut(&mut self, index: usize) -> &mut Self::Output {
         &mut self.e[index]
     }
 }
 
 impl AddAssign for Vec3 {
     fn add_assign(&mut self, rhs: Self) {
         self.e[0] += rhs.e[0];
         self.e[1] += rhs.e[1];
         self.e[2] += rhs.e[2];
     }
 }
 
 impl MulAssign<f64> for Vec3 {
     fn mul_assign(&mut self, rhs: f64) {
         self.e[0] *= rhs;
         self.e[1] *= rhs;
         self.e[2] *= rhs;
     }
 }
 
 impl DivAssign<f64> for Vec3 {
     fn div_assign(&mut self, rhs: f64) {
         self.mul_assign(1.0 / rhs);
     }
 }
 
 impl Display for Vec3 {
     fn fmt(&self, f: &mut std::fmt::Formatter<'_>) -> std::fmt::Result {
         write!(f, "{} {} {}", self.e[0], self.e[1], self.e[2])
     }
 }
 
 impl Add for Vec3 {
     type Output = Self;
 
     fn add(self, rhs: Self) -> Self::Output {
         Self::Output {
             e: [
                 self.e[0] + rhs.e[0],
                 self.e[1] + rhs.e[1],
                 self.e[2] + rhs.e[2],
             ],
         }
     }
 }
 
 impl Sub for Vec3 {
     type Output = Self;
 
     fn sub(self, rhs: Self) -> Self::Output {
         Self::Output {
             e: [
                 self.e[0] - rhs.e[0],
                 self.e[1] - rhs.e[1],
                 self.e[2] - rhs.e[2],
             ],
         }
     }
 }
 
 impl Mul for Vec3 {
     type Output = Self;
 
     fn mul(self, rhs: Self) -> Self::Output {
         Self::Output {
             e: [
                 self.e[0] * rhs.e[0],
                 self.e[1] * rhs.e[1],
                 self.e[2] * rhs.e[2],
             ],
         }
     }
 }
 
 impl Mul<f64> for Vec3 {
     type Output = Self;
 
     fn mul(self, rhs: f64) -> Self::Output {
         Self::Output {
             e: [self.e[0] * rhs, self.e[1] * rhs, self.e[2] * rhs],
         }
     }
 }
 
 impl Mul<Vec3> for f64 {
     type Output = Vec3;
 
     fn mul(self, rhs: Vec3) -> Self::Output {
         rhs.mul(self)
     }
 }
 
 impl Div<f64> for Vec3 {
     type Output = Self;
 
     fn div(self, rhs: f64) -> Self::Output {
         self * (1.0 / rhs)
     }
 }
 
 #[inline]
 pub fn dot(u: Vec3, v: Vec3) -> f64 {
     u.e[0] * v.e[0] + u.e[1] * v.e[1] + u.e[2] * v.e[2]
 }
 
 #[inline]
 pub fn cross(u: Vec3, v: Vec3) -> Vec3 {
     Vec3::new(
         u.e[1] * v.e[2] - u.e[2] * v.e[1],
         u.e[2] * v.e[0] - u.e[0] * v.e[2],
         u.e[0] * v.e[1] - u.e[1] * v.e[0],
     )
 }
 
 #[inline]
 pub fn unit_vector(v: Vec3) -> Vec3 {
     v / v.length()
 }
 
 #[inline]
 pub fn random_in_unit_disk() -> Vec3 {
     loop {
         let p = Vec3::new(
             rand::random_range(-1.0..1.0),
             rand::random_range(-1.0..1.0),
             0.0,
         );
         if p.length_squared() < 1.0 {
             return p;
         }
     }
 }

Listing 47: [vec3.rs] vec3 random utility functions

Then we need to figure out how to manipulate a random vector so that we only get results that are on the surface of a hemisphere. There are analytical methods of doing this, but they are actually surprisingly complicated to understand, and quite a bit complicated to implement. Instead, we'll use what is typically the easiest algorithm: A rejection method. A rejection method works by repeatedly generating random samples until we produce a sample that meets the desired criteria. In other words, keep rejecting bad samples until you find a good one.

There are many equally valid ways of generating a random vector on a hemisphere using the rejection method, but for our purposes we will go with the simplest, which is:

1. Generate a random vector inside the unit sphere
2. Normalize this vector to extend it to the sphere surface
3. Invert the normalized vector if it falls onto the wrong hemisphere

First, we will use a rejection method to generate the random vector inside the unit sphere (that is, a sphere of radius \( 1 \)). Pick a random point inside the cube enclosing the unit sphere (that is, where \( 𝑥 \), \( 𝑦 \), and \( 𝑧 \) are all in the range \( [−1,+1] \)). If this point lies outside the unit sphere, then generate a new one until we find one that lies inside or on the unit sphere.

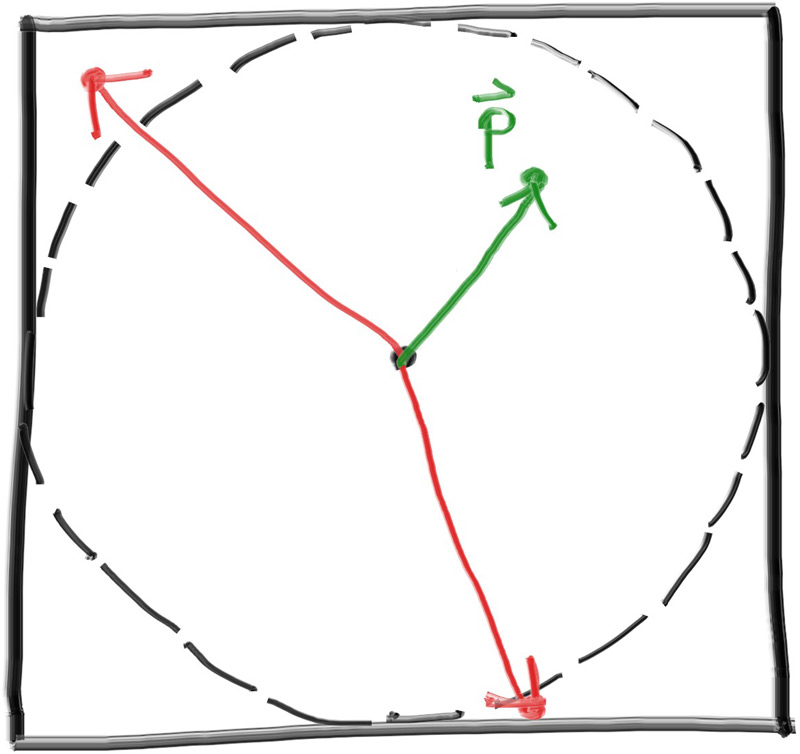
Figure 11: Two vectors were rejected before finding a good one (pre-normalization)

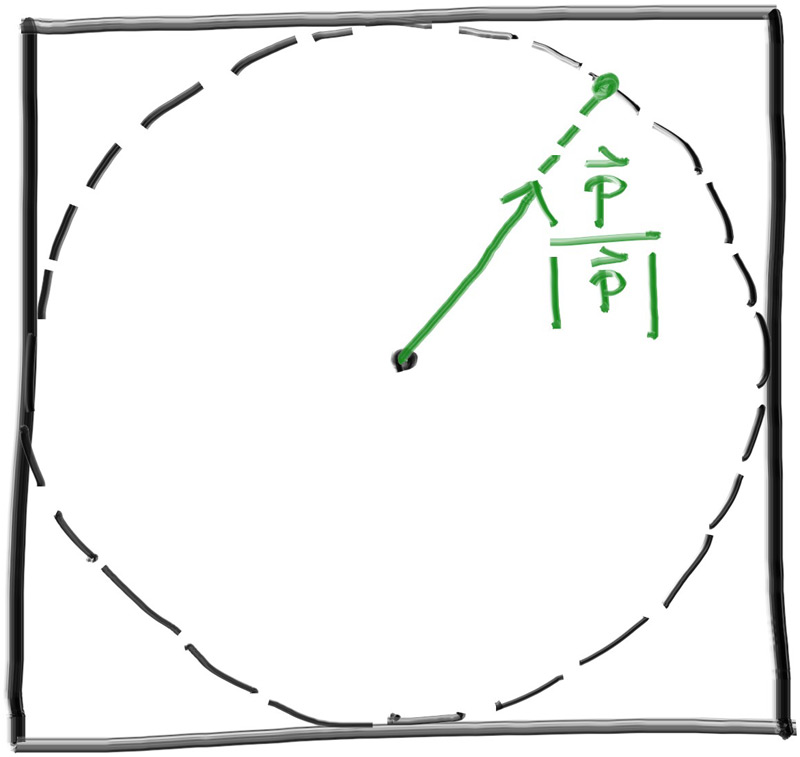
Figure 12: The accepted random vector is normalized to produce a unit vector

Here's our first draft of the function:

diff --git a/src/vec3.rs b/src/vec3.rs
index f9228ac..e3ee3ea 100644
--- a/src/vec3.rs
+++ b/src/vec3.rs
@@ -1,202 +1,213 @@
 use std::{
     fmt::Display,
     ops::{Add, AddAssign, Div, DivAssign, Index, IndexMut, Mul, MulAssign, Neg, Sub},
 };
 
 #[derive(Debug, Default, Clone, Copy)]
 pub struct Vec3 {
     pub e: [f64; 3],
 }
 
 pub type Point3 = Vec3;
 
 impl Vec3 {
     pub fn new(e0: f64, e1: f64, e2: f64) -> Self {
         Self { e: [e0, e1, e2] }
     }
 
     pub fn x(&self) -> f64 {
         self.e[0]
     }
 
     pub fn y(&self) -> f64 {
         self.e[1]
     }
 
     pub fn z(&self) -> f64 {
         self.e[2]
     }
 
     pub fn length(&self) -> f64 {
         f64::sqrt(self.length_squared())
     }
 
     pub fn length_squared(&self) -> f64 {
         self.e[0] * self.e[0] + self.e[1] * self.e[1] + self.e[2] * self.e[2]
     }
 
     pub fn random() -> Self {
         Vec3 { e: rand::random() }
     }
 
     pub fn random_range(min: f64, max: f64) -> Self {
         Vec3::new(
             rand::random_range(min..max),
             rand::random_range(min..max),
             rand::random_range(min..max),
         )
     }
 }
 
 impl Neg for Vec3 {
     type Output = Self;
 
     fn neg(self) -> Self::Output {
         Self::Output {
             e: self.e.map(|e| -e),
         }
     }
 }
 
 impl Index<usize> for Vec3 {
     type Output = f64;
 
     fn index(&self, index: usize) -> &Self::Output {
         &self.e[index]
     }
 }
 
 impl IndexMut<usize> for Vec3 {
     fn index_mut(&mut self, index: usize) -> &mut Self::Output {
         &mut self.e[index]
     }
 }
 
 impl AddAssign for Vec3 {
     fn add_assign(&mut self, rhs: Self) {
         self.e[0] += rhs.e[0];
         self.e[1] += rhs.e[1];
         self.e[2] += rhs.e[2];
     }
 }
 
 impl MulAssign<f64> for Vec3 {
     fn mul_assign(&mut self, rhs: f64) {
         self.e[0] *= rhs;
         self.e[1] *= rhs;
         self.e[2] *= rhs;
     }
 }
 
 impl DivAssign<f64> for Vec3 {
     fn div_assign(&mut self, rhs: f64) {
         self.mul_assign(1.0 / rhs);
     }
 }
 
 impl Display for Vec3 {
     fn fmt(&self, f: &mut std::fmt::Formatter<'_>) -> std::fmt::Result {
         write!(f, "{} {} {}", self.e[0], self.e[1], self.e[2])
     }
 }
 
 impl Add for Vec3 {
     type Output = Self;
 
     fn add(self, rhs: Self) -> Self::Output {
         Self::Output {
             e: [
                 self.e[0] + rhs.e[0],
                 self.e[1] + rhs.e[1],
                 self.e[2] + rhs.e[2],
             ],
         }
     }
 }
 
 impl Sub for Vec3 {
     type Output = Self;
 
     fn sub(self, rhs: Self) -> Self::Output {
         Self::Output {
             e: [
                 self.e[0] - rhs.e[0],
                 self.e[1] - rhs.e[1],
                 self.e[2] - rhs.e[2],
             ],
         }
     }
 }
 
 impl Mul for Vec3 {
     type Output = Self;
 
     fn mul(self, rhs: Self) -> Self::Output {
         Self::Output {
             e: [
                 self.e[0] * rhs.e[0],
                 self.e[1] * rhs.e[1],
                 self.e[2] * rhs.e[2],
             ],
         }
     }
 }
 
 impl Mul<f64> for Vec3 {
     type Output = Self;
 
     fn mul(self, rhs: f64) -> Self::Output {
         Self::Output {
             e: [self.e[0] * rhs, self.e[1] * rhs, self.e[2] * rhs],
         }
     }
 }
 
 impl Mul<Vec3> for f64 {
     type Output = Vec3;
 
     fn mul(self, rhs: Vec3) -> Self::Output {
         rhs.mul(self)
     }
 }
 
 impl Div<f64> for Vec3 {
     type Output = Self;
 
     fn div(self, rhs: f64) -> Self::Output {
         self * (1.0 / rhs)
     }
 }
 
 #[inline]
 pub fn dot(u: Vec3, v: Vec3) -> f64 {
     u.e[0] * v.e[0] + u.e[1] * v.e[1] + u.e[2] * v.e[2]
 }
 
 #[inline]
 pub fn cross(u: Vec3, v: Vec3) -> Vec3 {
     Vec3::new(
         u.e[1] * v.e[2] - u.e[2] * v.e[1],
         u.e[2] * v.e[0] - u.e[0] * v.e[2],
         u.e[0] * v.e[1] - u.e[1] * v.e[0],
     )
 }
 
 #[inline]
 pub fn unit_vector(v: Vec3) -> Vec3 {
     v / v.length()
 }
 
 #[inline]
+pub fn random_unit_vector() -> Vec3 {
+    loop {
+        let p = Vec3::random_range(-1.0, 1.0);
+        let lensq = p.length_squared();
+        if lensq <= 1.0 {
+            return p / f64::sqrt(lensq);
+        }
+    }
+}
+
+#[inline]
 pub fn random_in_unit_disk() -> Vec3 {
     loop {
         let p = Vec3::new(
             rand::random_range(-1.0..1.0),
             rand::random_range(-1.0..1.0),
             0.0,
         );
         if p.length_squared() < 1.0 {
             return p;
         }
     }
 }

Listing 48: [vec3.rs] The random_unit_vector() function, version one

Sadly, we have a small floating-point abstraction leak to deal with. Since floating-point numbers have finite precision, a very small value can underflow to zero when squared. So if all three coordinates are small enough (that is, very near the center of the sphere), the norm of the vector will be zero, and thus normalizing will yield the bogus vector \( [\pm \infty, \pm \infty, \pm \infty] \). To fix this, we'll also reject points that lie inside this “black hole” around the center. With double precision (64-bit floats), we can safely support values greater than 10−160.

Here's our more robust function:

diff --git a/src/vec3.rs b/src/vec3.rs
index e3ee3ea..ba86acc 100644
--- a/src/vec3.rs
+++ b/src/vec3.rs
@@ -1,213 +1,213 @@
 use std::{
     fmt::Display,
     ops::{Add, AddAssign, Div, DivAssign, Index, IndexMut, Mul, MulAssign, Neg, Sub},
 };
 
 #[derive(Debug, Default, Clone, Copy)]
 pub struct Vec3 {
     pub e: [f64; 3],
 }
 
 pub type Point3 = Vec3;
 
 impl Vec3 {
     pub fn new(e0: f64, e1: f64, e2: f64) -> Self {
         Self { e: [e0, e1, e2] }
     }
 
     pub fn x(&self) -> f64 {
         self.e[0]
     }
 
     pub fn y(&self) -> f64 {
         self.e[1]
     }
 
     pub fn z(&self) -> f64 {
         self.e[2]
     }
 
     pub fn length(&self) -> f64 {
         f64::sqrt(self.length_squared())
     }
 
     pub fn length_squared(&self) -> f64 {
         self.e[0] * self.e[0] + self.e[1] * self.e[1] + self.e[2] * self.e[2]
     }
 
     pub fn random() -> Self {
         Vec3 { e: rand::random() }
     }
 
     pub fn random_range(min: f64, max: f64) -> Self {
         Vec3::new(
             rand::random_range(min..max),
             rand::random_range(min..max),
             rand::random_range(min..max),
         )
     }
 }
 
 impl Neg for Vec3 {
     type Output = Self;
 
     fn neg(self) -> Self::Output {
         Self::Output {
             e: self.e.map(|e| -e),
         }
     }
 }
 
 impl Index<usize> for Vec3 {
     type Output = f64;
 
     fn index(&self, index: usize) -> &Self::Output {
         &self.e[index]
     }
 }
 
 impl IndexMut<usize> for Vec3 {
     fn index_mut(&mut self, index: usize) -> &mut Self::Output {
         &mut self.e[index]
     }
 }
 
 impl AddAssign for Vec3 {
     fn add_assign(&mut self, rhs: Self) {
         self.e[0] += rhs.e[0];
         self.e[1] += rhs.e[1];
         self.e[2] += rhs.e[2];
     }
 }
 
 impl MulAssign<f64> for Vec3 {
     fn mul_assign(&mut self, rhs: f64) {
         self.e[0] *= rhs;
         self.e[1] *= rhs;
         self.e[2] *= rhs;
     }
 }
 
 impl DivAssign<f64> for Vec3 {
     fn div_assign(&mut self, rhs: f64) {
         self.mul_assign(1.0 / rhs);
     }
 }
 
 impl Display for Vec3 {
     fn fmt(&self, f: &mut std::fmt::Formatter<'_>) -> std::fmt::Result {
         write!(f, "{} {} {}", self.e[0], self.e[1], self.e[2])
     }
 }
 
 impl Add for Vec3 {
     type Output = Self;
 
     fn add(self, rhs: Self) -> Self::Output {
         Self::Output {
             e: [
                 self.e[0] + rhs.e[0],
                 self.e[1] + rhs.e[1],
                 self.e[2] + rhs.e[2],
             ],
         }
     }
 }
 
 impl Sub for Vec3 {
     type Output = Self;
 
     fn sub(self, rhs: Self) -> Self::Output {
         Self::Output {
             e: [
                 self.e[0] - rhs.e[0],
                 self.e[1] - rhs.e[1],
                 self.e[2] - rhs.e[2],
             ],
         }
     }
 }
 
 impl Mul for Vec3 {
     type Output = Self;
 
     fn mul(self, rhs: Self) -> Self::Output {
         Self::Output {
             e: [
                 self.e[0] * rhs.e[0],
                 self.e[1] * rhs.e[1],
                 self.e[2] * rhs.e[2],
             ],
         }
     }
 }
 
 impl Mul<f64> for Vec3 {
     type Output = Self;
 
     fn mul(self, rhs: f64) -> Self::Output {
         Self::Output {
             e: [self.e[0] * rhs, self.e[1] * rhs, self.e[2] * rhs],
         }
     }
 }
 
 impl Mul<Vec3> for f64 {
     type Output = Vec3;
 
     fn mul(self, rhs: Vec3) -> Self::Output {
         rhs.mul(self)
     }
 }
 
 impl Div<f64> for Vec3 {
     type Output = Self;
 
     fn div(self, rhs: f64) -> Self::Output {
         self * (1.0 / rhs)
     }
 }
 
 #[inline]
 pub fn dot(u: Vec3, v: Vec3) -> f64 {
     u.e[0] * v.e[0] + u.e[1] * v.e[1] + u.e[2] * v.e[2]
 }
 
 #[inline]
 pub fn cross(u: Vec3, v: Vec3) -> Vec3 {
     Vec3::new(
         u.e[1] * v.e[2] - u.e[2] * v.e[1],
         u.e[2] * v.e[0] - u.e[0] * v.e[2],
         u.e[0] * v.e[1] - u.e[1] * v.e[0],
     )
 }
 
 #[inline]
 pub fn unit_vector(v: Vec3) -> Vec3 {
     v / v.length()
 }
 
 #[inline]
 pub fn random_unit_vector() -> Vec3 {
     loop {
         let p = Vec3::random_range(-1.0, 1.0);
         let lensq = p.length_squared();
-        if lensq <= 1.0 {
+        if 1e-160 < lensq && lensq <= 1.0 {
             return p / f64::sqrt(lensq);
         }
     }
 }
 
 #[inline]
 pub fn random_in_unit_disk() -> Vec3 {
     loop {
         let p = Vec3::new(
             rand::random_range(-1.0..1.0),
             rand::random_range(-1.0..1.0),
             0.0,
         );
         if p.length_squared() < 1.0 {
             return p;
         }
     }
 }

Listing 49: [vec3.rs] The random_unit_vector() function, version two

Now that we have a random unit vector, we can determine if it is on the correct hemisphere by comparing against the surface normal:

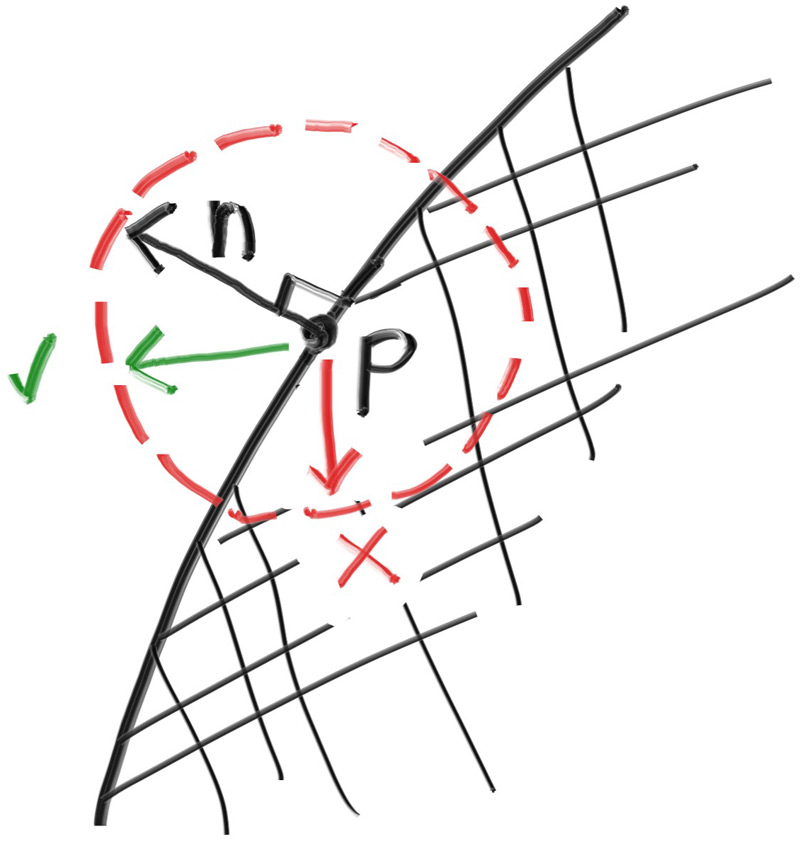
Figure 13: The normal vector tells us which hemisphere we need

We can take the dot product of the surface normal and our random vector to determine if it's in the correct hemisphere. If the dot product is positive, then the vector is in the correct hemisphere. If the dot product is negative, then we need to invert the vector.

diff --git a/src/vec3.rs b/src/vec3.rs
index ba86acc..4cb969b 100644
--- a/src/vec3.rs
+++ b/src/vec3.rs
@@ -1,213 +1,223 @@
 use std::{
     fmt::Display,
     ops::{Add, AddAssign, Div, DivAssign, Index, IndexMut, Mul, MulAssign, Neg, Sub},
 };
 
 #[derive(Debug, Default, Clone, Copy)]
 pub struct Vec3 {
     pub e: [f64; 3],
 }
 
 pub type Point3 = Vec3;
 
 impl Vec3 {
     pub fn new(e0: f64, e1: f64, e2: f64) -> Self {
         Self { e: [e0, e1, e2] }
     }
 
     pub fn x(&self) -> f64 {
         self.e[0]
     }
 
     pub fn y(&self) -> f64 {
         self.e[1]
     }
 
     pub fn z(&self) -> f64 {
         self.e[2]
     }
 
     pub fn length(&self) -> f64 {
         f64::sqrt(self.length_squared())
     }
 
     pub fn length_squared(&self) -> f64 {
         self.e[0] * self.e[0] + self.e[1] * self.e[1] + self.e[2] * self.e[2]
     }
 
     pub fn random() -> Self {
         Vec3 { e: rand::random() }
     }
 
     pub fn random_range(min: f64, max: f64) -> Self {
         Vec3::new(
             rand::random_range(min..max),
             rand::random_range(min..max),
             rand::random_range(min..max),
         )
     }
 }
 
 impl Neg for Vec3 {
     type Output = Self;
 
     fn neg(self) -> Self::Output {
         Self::Output {
             e: self.e.map(|e| -e),
         }
     }
 }
 
 impl Index<usize> for Vec3 {
     type Output = f64;
 
     fn index(&self, index: usize) -> &Self::Output {
         &self.e[index]
     }
 }
 
 impl IndexMut<usize> for Vec3 {
     fn index_mut(&mut self, index: usize) -> &mut Self::Output {
         &mut self.e[index]
     }
 }
 
 impl AddAssign for Vec3 {
     fn add_assign(&mut self, rhs: Self) {
         self.e[0] += rhs.e[0];
         self.e[1] += rhs.e[1];
         self.e[2] += rhs.e[2];
     }
 }
 
 impl MulAssign<f64> for Vec3 {
     fn mul_assign(&mut self, rhs: f64) {
         self.e[0] *= rhs;
         self.e[1] *= rhs;
         self.e[2] *= rhs;
     }
 }
 
 impl DivAssign<f64> for Vec3 {
     fn div_assign(&mut self, rhs: f64) {
         self.mul_assign(1.0 / rhs);
     }
 }
 
 impl Display for Vec3 {
     fn fmt(&self, f: &mut std::fmt::Formatter<'_>) -> std::fmt::Result {
         write!(f, "{} {} {}", self.e[0], self.e[1], self.e[2])
     }
 }
 
 impl Add for Vec3 {
     type Output = Self;
 
     fn add(self, rhs: Self) -> Self::Output {
         Self::Output {
             e: [
                 self.e[0] + rhs.e[0],
                 self.e[1] + rhs.e[1],
                 self.e[2] + rhs.e[2],
             ],
         }
     }
 }
 
 impl Sub for Vec3 {
     type Output = Self;
 
     fn sub(self, rhs: Self) -> Self::Output {
         Self::Output {
             e: [
                 self.e[0] - rhs.e[0],
                 self.e[1] - rhs.e[1],
                 self.e[2] - rhs.e[2],
             ],
         }
     }
 }
 
 impl Mul for Vec3 {
     type Output = Self;
 
     fn mul(self, rhs: Self) -> Self::Output {
         Self::Output {
             e: [
                 self.e[0] * rhs.e[0],
                 self.e[1] * rhs.e[1],
                 self.e[2] * rhs.e[2],
             ],
         }
     }
 }
 
 impl Mul<f64> for Vec3 {
     type Output = Self;
 
     fn mul(self, rhs: f64) -> Self::Output {
         Self::Output {
             e: [self.e[0] * rhs, self.e[1] * rhs, self.e[2] * rhs],
         }
     }
 }
 
 impl Mul<Vec3> for f64 {
     type Output = Vec3;
 
     fn mul(self, rhs: Vec3) -> Self::Output {
         rhs.mul(self)
     }
 }
 
 impl Div<f64> for Vec3 {
     type Output = Self;
 
     fn div(self, rhs: f64) -> Self::Output {
         self * (1.0 / rhs)
     }
 }
 
 #[inline]
 pub fn dot(u: Vec3, v: Vec3) -> f64 {
     u.e[0] * v.e[0] + u.e[1] * v.e[1] + u.e[2] * v.e[2]
 }
 
 #[inline]
 pub fn cross(u: Vec3, v: Vec3) -> Vec3 {
     Vec3::new(
         u.e[1] * v.e[2] - u.e[2] * v.e[1],
         u.e[2] * v.e[0] - u.e[0] * v.e[2],
         u.e[0] * v.e[1] - u.e[1] * v.e[0],
     )
 }
 
 #[inline]
 pub fn unit_vector(v: Vec3) -> Vec3 {
     v / v.length()
 }
 
 #[inline]
 pub fn random_unit_vector() -> Vec3 {
     loop {
         let p = Vec3::random_range(-1.0, 1.0);
         let lensq = p.length_squared();
         if 1e-160 < lensq && lensq <= 1.0 {
             return p / f64::sqrt(lensq);
         }
     }
 }
 
 #[inline]
+pub fn random_on_hemisphere(normal: Vec3) -> Vec3 {
+    let on_unit_sphere = random_unit_vector();
+    if dot(on_unit_sphere, normal) > 0.0 {
+        on_unit_sphere
+    } else {
+        -on_unit_sphere
+    }
+}
+
+#[inline]
 pub fn random_in_unit_disk() -> Vec3 {
     loop {
         let p = Vec3::new(
             rand::random_range(-1.0..1.0),
             rand::random_range(-1.0..1.0),
             0.0,
         );
         if p.length_squared() < 1.0 {
             return p;
         }
     }
 }

Listing 50: [vec3.rs] The random_on_hemisphere() function

If a ray bounces off of a material and keeps 100% of its color, then we say that the material is white. If a ray bounces off of a material and keeps 0% of its color, then we say that the material is black. As a first demonstration of our new diffuse material we'll set the ray_color function to return 50% of the color from a bounce. We should expect to get a nice gray color.

diff --git a/src/camera.rs b/src/camera.rs
index f181b03..181eb64 100644
--- a/src/camera.rs
+++ b/src/camera.rs
@@ -1,151 +1,152 @@
 use crate::{hittable::Hittable, prelude::*};
 
 pub struct Camera {
     /// Ratio of image width over height
     pub aspect_ratio: f64,
     /// Rendered image width in pixel count
     pub image_width: i32,
     // Count of random samples for each pixel
     pub samples_per_pixel: i32,
 
     /// Rendered image height
     image_height: i32,
     // Color scale factor for a sum of pixel samples
     pixel_samples_scale: f64,
     /// Camera center
     center: Point3,
     /// Location of pixel 0, 0
     pixel00_loc: Point3,
     /// Offset to pixel to the right
     pixel_delta_u: Vec3,
     /// Offset to pixel below
     pixel_delta_v: Vec3,
 }
 
 impl Default for Camera {
     fn default() -> Self {
         Self {
             aspect_ratio: 1.0,
             image_width: 100,
             samples_per_pixel: 10,
             image_height: Default::default(),
             pixel_samples_scale: Default::default(),
             center: Default::default(),
             pixel00_loc: Default::default(),
             pixel_delta_u: Default::default(),
             pixel_delta_v: Default::default(),
         }
     }
 }
 
 impl Camera {
     pub fn with_aspect_ratio(mut self, aspect_ratio: f64) -> Self {
         self.aspect_ratio = aspect_ratio;
 
         self
     }
 
     pub fn with_image_width(mut self, image_width: i32) -> Self {
         self.image_width = image_width;
 
         self
     }
 
     pub fn with_samples_per_pixel(mut self, samples_per_pixel: i32) -> Self {
         self.samples_per_pixel = samples_per_pixel;
 
         self
     }
 
     pub fn render(&mut self, world: &impl Hittable) -> std::io::Result<()> {
         self.initialize();
 
         println!("P3");
         println!("{} {}", self.image_width, self.image_height);
         println!("255");
 
         for j in 0..self.image_height {
             info!("Scanlines remaining: {}", self.image_height - j);
             for i in 0..self.image_width {
                 let mut pixel_color = Color::new(0.0, 0.0, 0.0);
                 for _sample in 0..self.samples_per_pixel {
                     let r = self.get_ray(i, j);
                     pixel_color += Self::ray_color(r, world);
                 }
                 write_color(std::io::stdout(), self.pixel_samples_scale * pixel_color)?;
             }
         }
         info!("Done.");
 
         Ok(())
     }
 
     fn initialize(&mut self) {
         self.image_height = {
             let image_height = (self.image_width as f64 / self.aspect_ratio) as i32;
             if image_height < 1 { 1 } else { image_height }
         };
 
         self.pixel_samples_scale = 1.0 / self.samples_per_pixel as f64;
 
         self.center = Point3::new(0.0, 0.0, 0.0);
 
         // Determine viewport dimensions.
         let focal_length = 1.0;
         let viewport_height = 2.0;
         let viewport_width =
             viewport_height * (self.image_width as f64) / (self.image_height as f64);
 
         // Calculate the vectors across the horizontal and down the vertical viewport edges.
         let viewport_u = Vec3::new(viewport_width, 0.0, 0.0);
         let viewport_v = Vec3::new(0.0, -viewport_height, 0.0);
 
         // Calculate the horizontal and vertical delta vectors from pixel to pixel.
         self.pixel_delta_u = viewport_u / self.image_width as f64;
         self.pixel_delta_v = viewport_v / self.image_height as f64;
 
         // Calculate the location of the upper left pixel.
         let viewport_upper_left =
             self.center - Vec3::new(0.0, 0.0, focal_length) - viewport_u / 2.0 - viewport_v / 2.0;
         self.pixel00_loc = viewport_upper_left + 0.5 * (self.pixel_delta_u + self.pixel_delta_v);
     }
 
     fn get_ray(&self, i: i32, j: i32) -> Ray {
         // Construct a camera ray originating from the origin and directed at randomly sampled
         // point around the pixel location i, j.
 
         let offset = Self::sample_square();
         let pixel_sample = self.pixel00_loc
             + ((i as f64 + offset.x()) * self.pixel_delta_u)
             + ((j as f64 + offset.y()) * self.pixel_delta_v);
 
         let ray_origin = self.center;
         let ray_direction = pixel_sample - ray_origin;
 
         Ray::new(ray_origin, ray_direction)
     }
 
     fn sample_square() -> Vec3 {
         // Returns the vector to a random point in the [-.5,-.5]-[+.5,+.5] unit square.
         Vec3::new(
             rand::random::<f64>() - 0.5,
             rand::random::<f64>() - 0.5,
             0.0,
         )
     }
 
     fn _sample_disk(radius: f64) -> Vec3 {
         // Returns a random point in the unit (radius 0.5) disk centered at the origin.
         radius * random_in_unit_disk()
     }
 
     fn ray_color(r: Ray, world: &impl Hittable) -> Color {
         if let Some(rec) = world.hit(r, Interval::new(0.0, INFINITY)) {
-            return 0.5 * (rec.normal + Color::new(1.0, 1.0, 1.0));
+            let direction = random_on_hemisphere(rec.normal);
+            return 0.5 * Self::ray_color(Ray::new(rec.p, direction), world);
         }
 
         let unit_direction = unit_vector(r.direction());
         let a = 0.5 * (unit_direction.y() + 1.0);
         (1.0 - a) * Color::new(1.0, 1.0, 1.0) + a * Color::new(0.5, 0.7, 1.0)
     }
 }

Listing 51: [camera.rs] ray_color() using a random ray direction

... Indeed we do get rather nice gray spheres:

Image 7: First render of a diffuse sphere